Maximum Likelihood Estimation (MLE)

The maximum likelihood estimation approach to quantum state tomography calculates the state with the highest probability of producing the observed measurements. Specifically, it is the state which maximizes the likelihood function or equivalently, minimizes the negative log of this function:

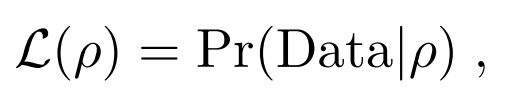
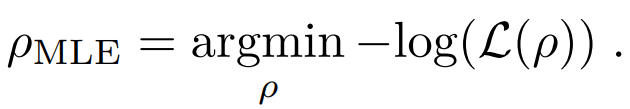
Likelihood Function MLE Estimate

1 Detector per Qubit

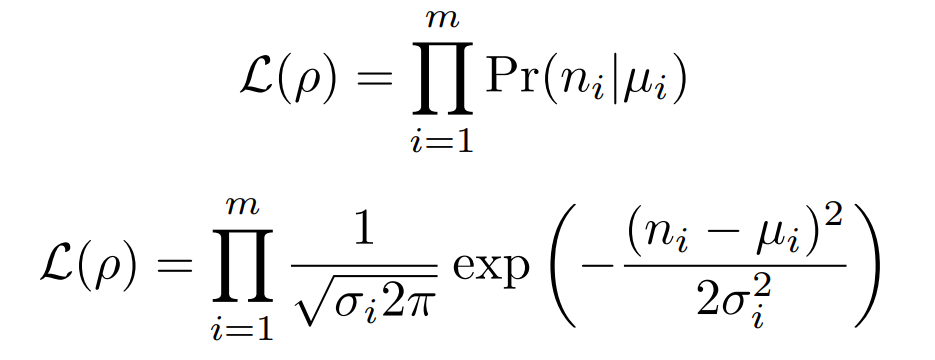
Log Likelihood Function 1 Det per Qubit

Ignoring the normalization factor, plugging in the variance, and taking the log of this function we get the following:

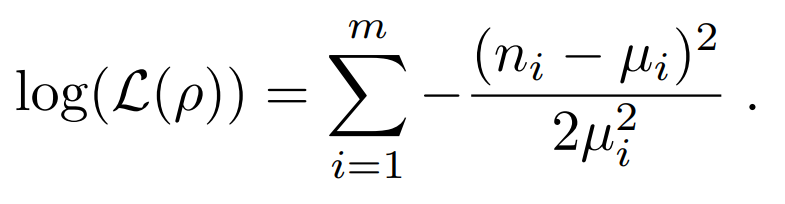
Log Likelihood Function 1 Det per Qubit

Definitions

  • ρ : Quantum state in density matrix form.
  • ni : Number of counts on measurement i.
  • μi : Expected number of counts on measurement i given ρ. More info can be found on the State Tomography page.
  • i ∈ [1,m], where m = Number of Measurements.

2 Detector per Qubit

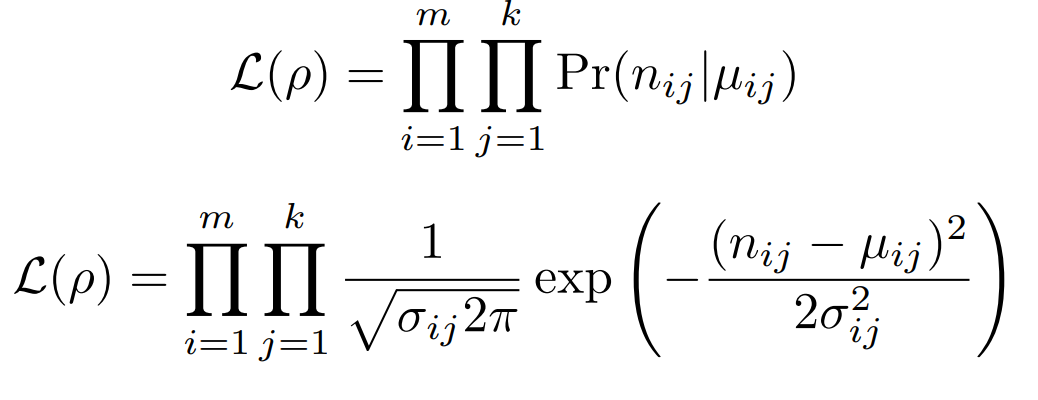
Log Likelihood Function 1 Det per Qubit

Ignoring the normalization factor, plugging in the variance, and taking the log of this function we get the following:

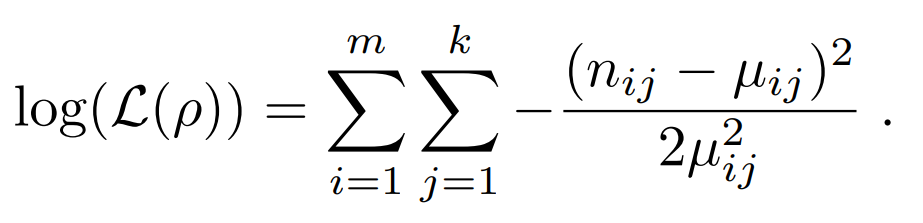
Log Likelihood Function 2 Det per Qubit

Definitions

  • ρ : Quantum state in density matrix form.
  • nij : Number of counts on measurement i for detector pair j.
  • μij : Expected number of counts on measurement i, detector j given ρ. More info can be found on the State Tomography page.
  • i ∈ [1,m], where m = Number of Measurements.
  • j ∈ [1,k], where k = Number of Detector pairs, which is equal to the number of qubits squared.

Optimization and T-Values

During the optimization we parameterize the density matrix as follows in order to ensure we are only considering valid density matrices:

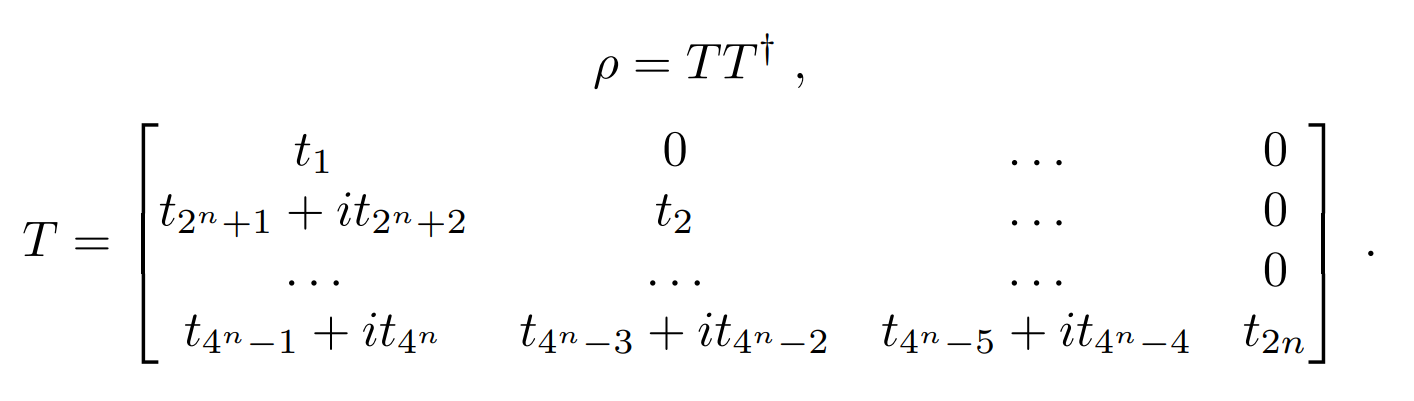
T-Values

The functions t_to_density(tvals) and density2t(rho) are used to convert t-values to and from a density matrix.

Hedged Maximum Likelihood Estimation (HMLE)

Hedged maximum likelihood is a simple modification of the maximum likelihood approach. This is available in our python code but not available on our state tomography interface. This procedure utilizes Lidstone's law, and hedges the estimate against un-seen possibilities. Instead of maximizing the likelihood, the estimate is the one that maximizes the product of the likelihood with the following hedge function:

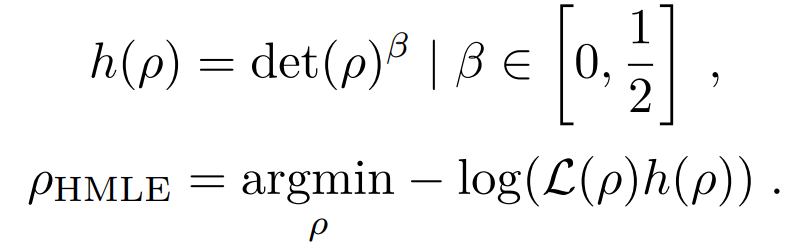
HMLE Estimate

The value of Beta can be defined in the conf settings; default is 1/2. Robin Blume-Kohout covers the hedged likelihood function in more detail in the paper titled Hedged Maximum Likelihood Estimation.

Words in bold correspond to variables defined in the source code.

Reference Papers