Table of Contents
- State Tomography
- Error Corrections
- Examples
State Tomography
State tomography starts with measuring the quantum state in a complete basis of measurements. Given the measurement data we wish to determine the best possible estimate for the quantum state. Using Bayes’ theorem we can define the probability of the state (ρ) given the data:
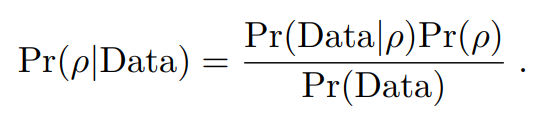
There are a variety of methods we can use to find an estimate for the state ρ, the most common of which is the maximum likelihood approach, the default method of our library.
Distribution of Counts
The counts of the measurements can be modeled by a Poisson Distribution. With high enough counts we can approximate this with a Normal Distribution using the Central Limit Theorem(CLT). A important fact of the poisson distribution is the variance is equal to the mean. Derivation of the model used is covered in Photonic State Tomography by Joe Altepeter.
1 Detector per Qubit
For each measurement we have 1 count number. For tomography on a single qubit using one detector, the counts are the singles on the detector. For two qubits and two detectors, the counts are the coincidences between the two detectors. The mean number of counts follows:
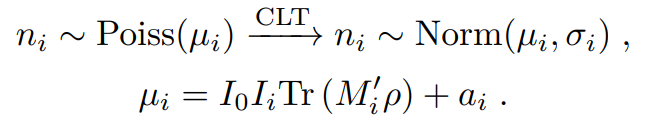
Definitions
- ρ : Quantum state in density matrix form.
- ni : Number of counts on measurement i.
- μi : Expected number of counts on measurement i given ρ.
- σi : Standard Deviation for the number of counts on measurement i given ρ. Equal to the square root of μi assuming a poisson distribution.
- I0 : The overall intensity initially approximated using linear tomography.
- Ii : The intensities of measurement i, which can be given as in input using drift correction. Default is 1.
- M'i : Measurement i with cross talk correction.
- ai : Predicted accidentals counts for measurement i. More info can be found on the accidental correction page.
- Tr(x) : The trace of input matrix x.
- i ∈ [1,m], where m = Number of Measurements.
2 Detector per Qubit
For each measurement we have 2N count numbers, N being the number of qubits. For tomography on a single qubit using two detectors, the counts are the singles on each detector. For two qubits and four detectors, the counts are the coincidences for each detector pair. For more details see the 2 qubits 4 detectors example. The mean number of counts follows:
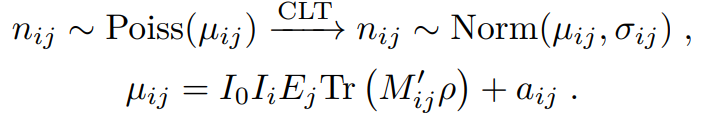
Definitions
- ρ : Quantum state in density matrix form.
- nij : Number of counts on measurement i for detector pair j.
- μij : Expected number of counts on measurement i, detector j given ρ.
- σij : Standard Deviation for the number of counts on measurement i, detector j given ρ. Equal to the square root of μij assuming a poisson distribution.
- I0 : The overall intensity initially approximated using linear tomography.
- Ii : The intensities of measurement i, which can be given as in input using drift correction. Default is 1.
- Ej : The relative efficiency on the jth detector pair. Default is 1.
- M'ij : jth basis of measurement i with cross talk correction.
- aij : Predicted accidentals counts for measurement i and detector pair j. More info can be found on the accidental correction page.
- Tr(x) : The trace of input matrix x.
- i ∈ [1,m], where m = Number of Measurements.
- j ∈ [1,k], where k = Number of Detector pairs, which is equal to the number of qubits squared.
Words in bold correspond to variables defined in the source code.